
HOME雑記帳(あすなろ)あすなろ199 かけられる数×かける数
あすなろ199 かけられる数×かける数
2018年5月25日投稿
2018.05号
ニセ科学という言葉があります。
私もこれまで時折、この手のものを俎上に上げて叩いてきたのですが、
そう思って自分の文章を読み返してみると、
10年ほど前は「エセ科学」と書いていました。
その頃はまだ、今のような定型句が無かったということなのだろうと思います。
さて、個人的に最近注目の科学雑誌……というか、理科雑誌があるのですが、
その4月号の特集が、
「ニセ科学を斬る! 2018」
というものでしたので、試しに買ってみました。
そうしたらですね、その一本目がコレ。
「『かけ算には順序がある』と教える教師たち ~正解が×にされる不条理」
名前をさらしますと、投稿者は山本弘氏。
山本氏の名前は、二十年以上前から知っております。
「と学会」という集まりを立ち上げて、
「トンデモ科学」を見つけてきては世に晒すということをしていて、
中々面白くて好きだったのですが、今回の山本氏には心底ガッカリですわホント。
この雑誌も、他の記事やバックナンバーは面白かったのになあ……。
ネットで調べてみると、この問題は結構前からずっと論争になっていたようです。
私も以前、チラリとこの手の話を聞いたことがあったのですが、
ウィキペディアで「かけ算の順序問題」なんて項目ができるほどの
ガチ論争になっているとは思ってもいませんでした。
まずは、これがどういう問題なのかをご紹介します。
問題「5円玉が3枚でいくらか」
・「5×3=15」→正解
・「3×5=15」→不正解
→3×5がバツなのは納得いかない!
で、問題を論じているサイトに行くと、皆様賢い方ばかりなのか、
無駄に難しい言葉で長々と難しく論じる人の多いこと多いこと。
もっと普通に書けばいいのに。
こういうレッテル貼りはあまり好きでは無いのですが、
この納得いかない派の人たちの理屈を読む限り、
あまり数学が好きではなかった方が多いようです。
また、「ナンセンス」などという、
もう50年前に流行した死語も頻繁に登場しますので、
反体制がカッコイイという時代に育ったご老人が多いのでしょうか。
ただ、逆に「順序が大切派」の理屈も、どうもフニャフニャしているんでよね。
簡単にまとめると、納得いかない派は、
「数学的では無い」
「社会では役に立たない」
という論調に対して、順序守る派は
「教育上」
「約束になっている」
「合理的である」
という主張なので、全くかみ合ってないのです。
さて、納得行かない派の中で、最も多く登場する用語が「交換法則」、
つまりかけ算は、順を入れかえても同じというアレです。
交換法則により順序は決まってないはずだ、
交換法則を習うときに混乱する、
数学的ではないからおかしい、
などなど。
ああそうですかー。
そんなにおっしゃるならば、納得いかない派の大好きな、
「数学的」という方面からお話してみましょうか。
数学というものは、全ての学問の中で、最も理屈に厳しい学問です。
他の科学では、事実を基にして仮設を立てたあとは、
それが一般的に正しいかは実験によって確認され、
反例が出ないときは正しいとされます。
しかし数学の場合。
例えば円周率は循環しない数ですが、他の科学のように
「誰が実験(計算)しても循環しなかったので、循環しないといえる」
などという曖昧な決め方は認められません。
例えば1兆桁まで計算して見つからなくても、
次の桁で見つかる可能性がゼロでない以上は、絶対にダメなのです。
今回のかけ算問題は、そういった数学の
「細かさ」
「うるささ」
に触れる第一歩である、と言えます。
「aがn個あるとき、a×nと定義する」
これが、日本の教育におけるかけ算の定義です。
定義なのです。
ここから外れることは許されません。
しかし後に、順序は指摘されなくなります。
定義を十分に理解した後は、
新たな公式を活用することで、
解答する速度を優先させるようになるからです。
今回の話でいうと、
その公式にあたるのが交換法則ですね。
逆に、
次の段階に進むまでは、
定義に従わなければいけないのです。
算数・数学とは、ある意味そういう訓練なのですから。
小学校のかけ算に限りません。
まだたくさん例はあります。
皆さん忘れているだけです。
例えば、中学一年で習う、一次方程式です。
方程式を解く際に、移項をしますよね。
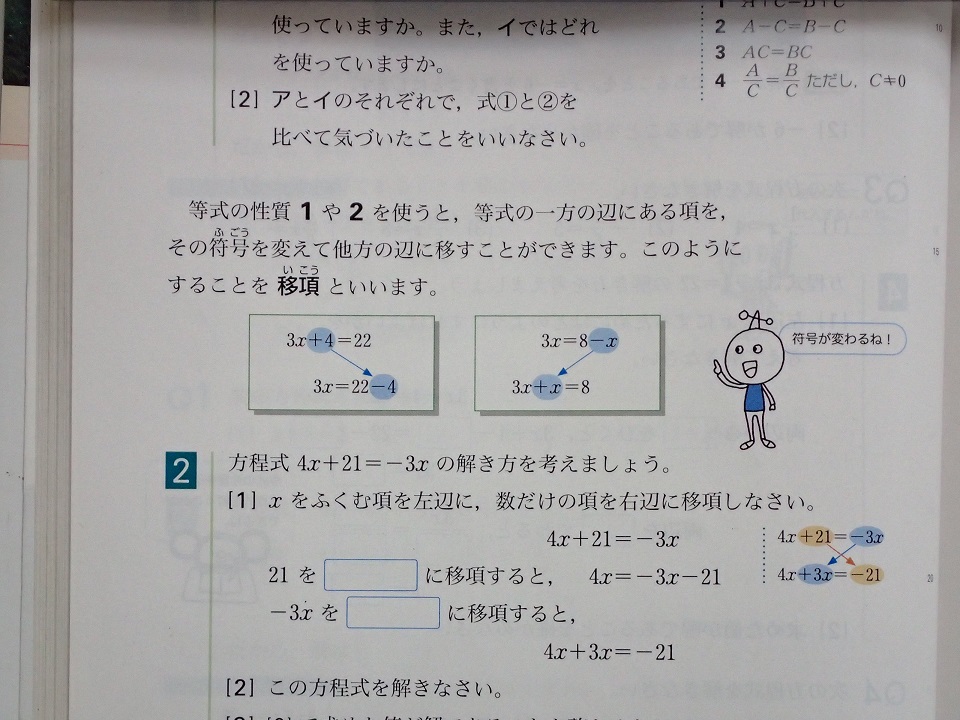
しかしこれは、定義に従った計算法ではありません。
定義に従った計算法は、
「両辺に同じ数を加える」などの
「等式の性質」を利用したものとなります。

移項を習う前のこの時点で、
移項を使って解いたら当然バツです。
定義に従っていないからです。
これは、
かけ算の順序を守らないとバツなのと、
同じことなのです。
移項を習ったあとは、移項でかまいません。
公式を使って、計算速度を優先させるからです。
他にもあります。
高校二年で微分を習うとき、最初に登場するのは極限値を使った導関数の計算です。
これが定義に従った微分法です。

微分の公式
「xのn乗の微分=nxのn-1乗」
を知っていても、ここで使ってはいけません。

それは計算上の公式であって、
定義に従っていないからです。
さらに、web上の意見では、
「大学生がマルで小学生がバツなんてものはあってはいけない」
なんてものもありましたが、では図形の証明はどうでしょうか。
高校入試の数学の問題では、
三角形の合同証明には
合同条件をきっちり書かないと減点です。

しかし、大学レベルになると、
三角形の合同条件なんていちいち書きません。
書いたとしても、「①②③から合同である」程度です。
というわけで、
大学生がマルで中学生がバツの例、ありますね。
そうそう。
一番笑ったのが、
「一律に×にしてしまうと、自由な発想がはぐくまれない」
などという反対論。
数学では、
ルールから外れた自由な発想などというものは
求められていません。
数学とは、たった一つの正解を求める学問なのです。
よく、
「国語では正解は一つでは無い」
とか言っちゃったりして、
「社会に出れば正解の無い問題はいっぱいある云々」
というお説教を始めちゃう人がいますが、
それは違います。
社会に出たからこそ、正解と不正解は、厳密に区別しなければいけません。
仮にどんな理不尽なルールであろうとも、
そこから外れた行動は、
そのルールがある以上は不正解なのです。
そのルールの範囲内で行動するのが、オトナというものなのです。
こんなものは、
制限速度や一時停止などの交通法規を出すまでもないですよね。
算数や数学によって、
「決まりに従うこと」と、
「間違いを間違いと認めること」を
学んでいただきたいと思います。
反対派の言い訳は、読んでいて見苦しいです。
学塾ヴィッセンブルク 朝倉智義
追記
ちょっと考え方を変えるとわかるのですが、
「用意するもの・・・3×鉛筆」
と、
「用意するもの・・・鉛筆×3」
では、
別にどっちでも同じと思いますか?
普通は、
上の書き方に違和感を感じると思うのですが。
ですからやはり、
日本においては、かける数が後なのです。
ところで、西洋諸国では、
かける数とかけられず数の順序を、
日本とは逆に教えているそうです。
しかしこれは、言語の構成上の問題だと思います。
例えば日本では、
「鉛筆3本」
と表記しますが、英語圏では
「3 鉛筆」(three pencils)
と表現するからです。
確かに日本語でも「3本の鉛筆」という言い方はありますが、
その場合は助詞「の」を伴う必要があります。
これに関連するお話は、
以前にも、さらにもっと以前にも
書いたことがあります。