HOME雑記帳(あすなろ)あすなろ215 東京2020エンブレム
あすなろ215 東京2020エンブレム
2019年12月13日投稿
2019.09号
そろそろ見慣れてきた、今度の東京オリンピックのエンブレムのお話です。

エンブレムについては、最初の「選考」の時に色々とケチがついたのはご存じの通りです。
そんないきさつを見ていましたから、今回のデザインが選ばれたときも
「一番つまんねえやつかよ」
「ABCDのうちのAってことは、最初から決まってたなこれは」
などという見方をしておりました。
ちなみに、キャラクターの方も、
「アイウのうちのア」
が選ばれていますので、こっちも「またかよ」って感じでした。
しかしですね、実はこのエンブレム、すごいデザインだったのです。
その討論がなされたのは、ツイッター上でした。
最初、どこかの大学教授が解析したというものがこちらです。
合同な三種類の長方形で成り立っているのですが、それが幾何学的に綺麗に組み合わさっている法則を示した図です。
当初はこのように、二十四角形の組み合わせと考えられていました。
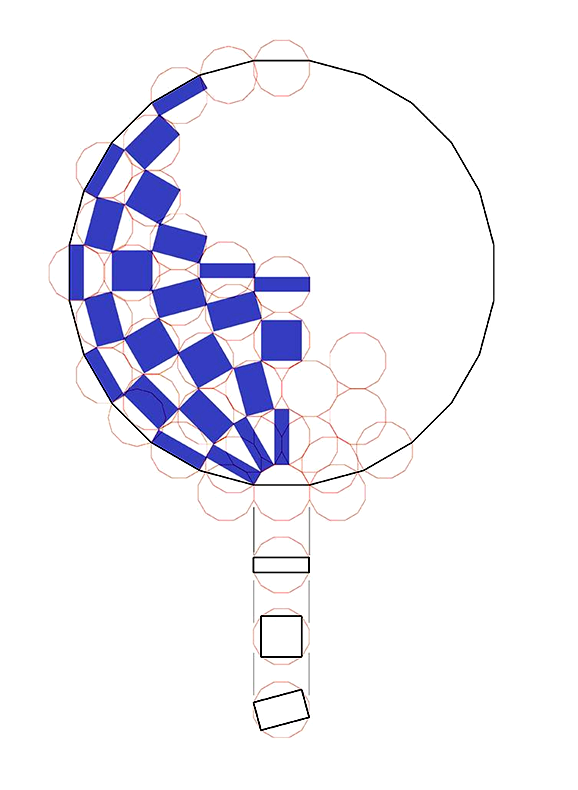

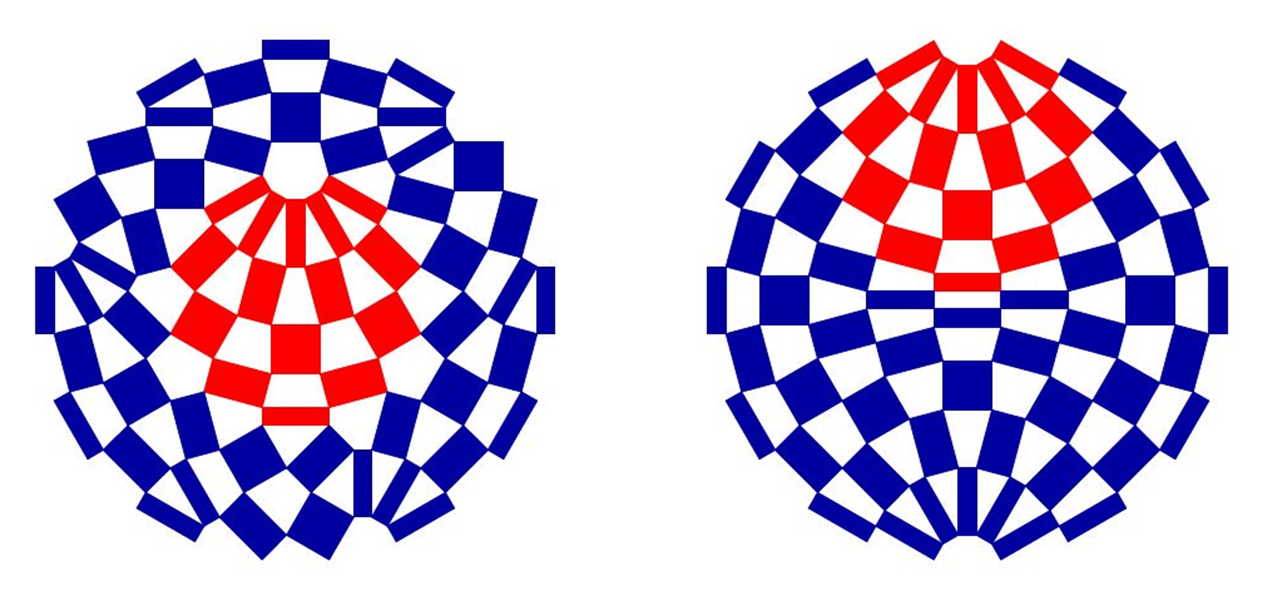
パラリンピックの方は見ての通り線対称図形ですが、オリンピックの方は線対称でも点対称でもありません……が、実は120度の回転対称な図形でした。
※点対称=180度の回転で重なる図形。
それに対して今回の図形は、120度の回転で重なる図形となっています。
それをわかりやすくしたのが次の図です。
偶然ながら、グーグルクロムのデザインにぴったり収まっています。

また、2つの図の抜けている円の部分は、同じ径の円となっていました。

2つの図を構成する長方形の個数は、共に大が9個、中が18個、小が18個で同じです。
それどころか、全て同じ向きのまま平行移動させるだけで、2つの図ができることも発見されました。
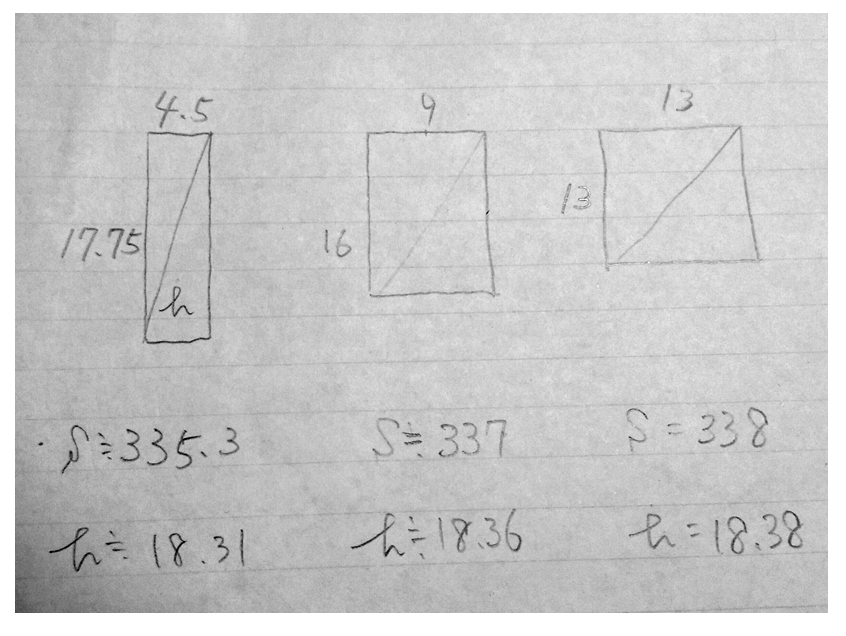
そして、これを構成する長方形については、対角線と面積が同じではないかという意見がこちらです。
面積は後に否定されますが、対角線の長さは確かにどれも同じでした。
最終的に、この三種類の長方形は、それぞれの対角線が30度・60度・90度で交わるものだということが見つかっています。
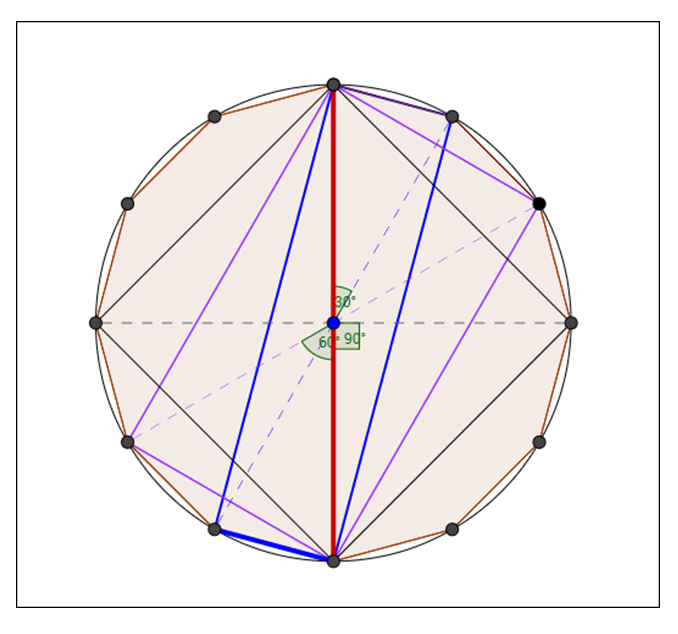
長方形の対角線をrとしたときの面積まで求められていました。
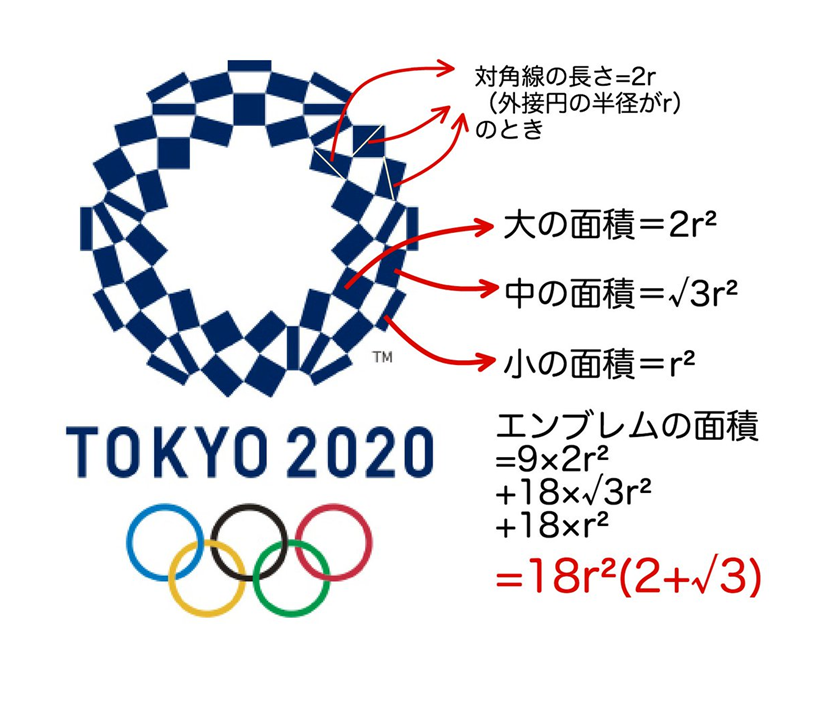
また、こんなものも見つかっています。
各長方形は、全てが頂点同士でつながっているのですが、抜けている円の部分は、接続される頂点の位置まで同じなのです。
頂点同士がぴったりとつながっています。
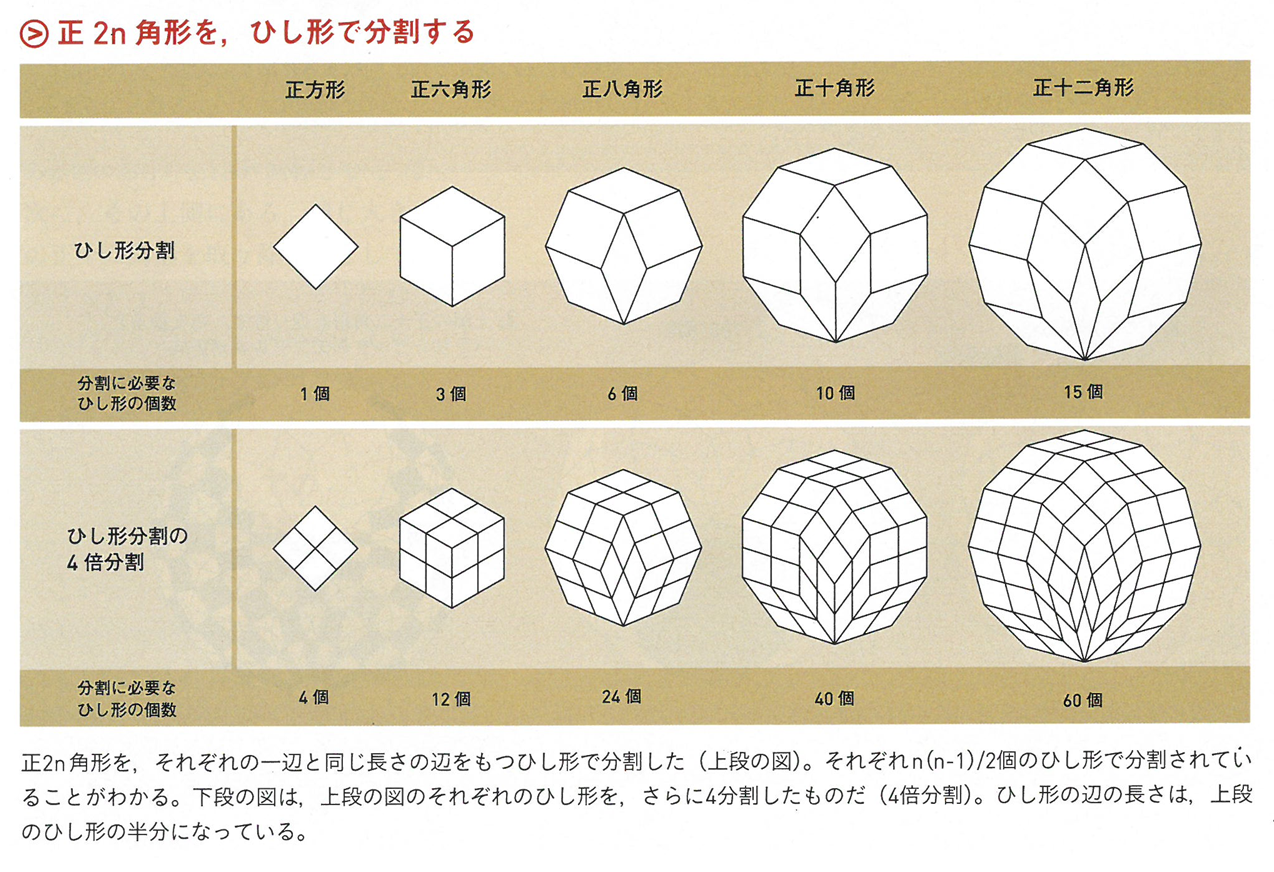
そして最終的に、この長方形の図案の元となった図形が、この菱形の組み合わせだと解析されています。

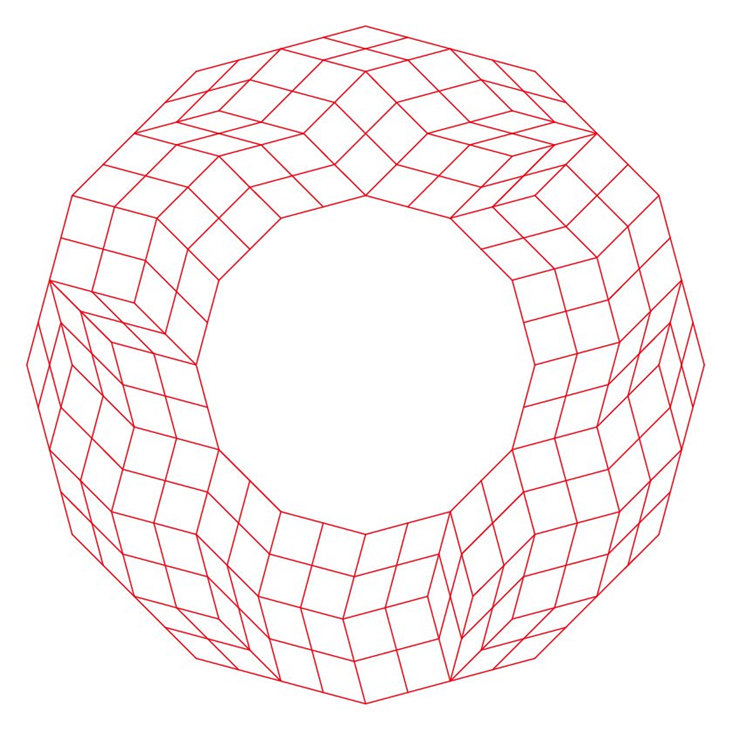
それを並び替えると、規則性のある綺麗な図形が浮かび上がります。
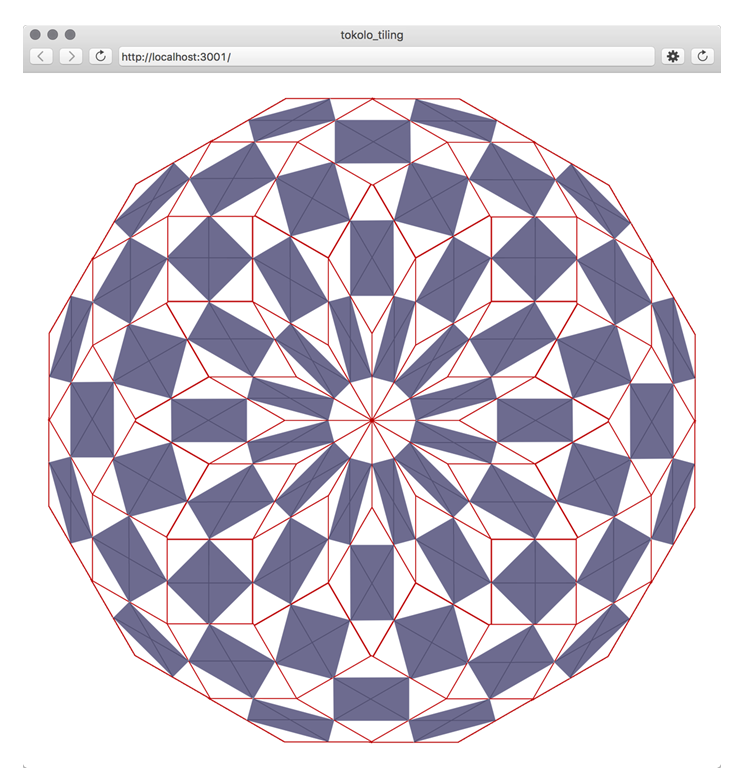
そして、これがどうやら「正解」のようです。
科学雑誌ニュートンの2019年9月号では、このような解析がなされていました。
(手持ちの本をスキャンしたので、ちょっと斜めになっているのはご容赦を)
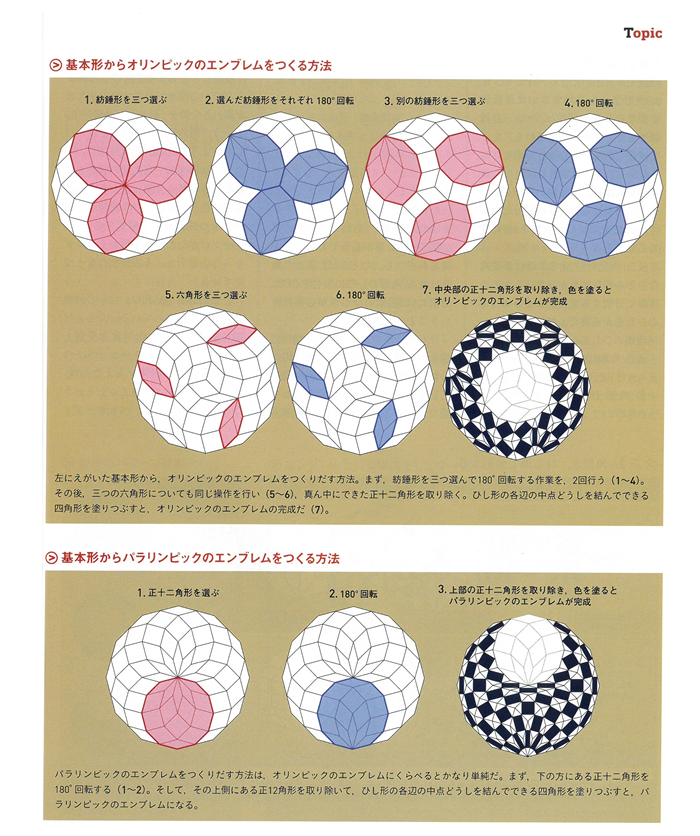
ところで、作者の野老(ところ)氏は、本当はこのように作ったわけではありません。
厚紙とテープを使って、文字通り手作業で作っていったのが原型なのだそうです。

さて、私がこの手の科学的要素の高い内容を紹介する時は、原則として本人の書いた論文を必ず読むようにしています。
まとめサイトやネット記事を見れば要点はわかるのですが、それでは本質が掴めないからです。
本人の書いた文章は、氏名+pdfで検索すると、普通はすぐにヒットします。
ところが、今回の主役である野老氏は、その手の論文を書いていないどころか、著作や寄稿すら見つかりませんでした。
そこで、今回の記事は、ニュートンの特集記事と、ネット上に散らばるまとめ記事、さらにはその元ネタとなったツイッターからなっています。
数少ない本人の弁としては、ニュートンのインタビュー記事があるのですが、それによると、数学好きの人には見つけられなかった秘密がまだありました。
それは、色です。
この図の三種類の長方形の面積比は、およそ100:86:50となっているのですが、そこからシアン:マゼンダ:イエロー:黒の比を100:86:0:50で混ぜた藍色を用いて、この原案を作ったのだそうです。
※原案ではC100、M86、Y0、K50でしたが、実際のエンブレムではM80となっています。
また野老氏は、同じパターンを用いることで、オリンピック関連イベントのエンブレムも作り上げています。

この様子でしたら、まだまだ他にも応用の利きそうなデザインですね。
ここまで読んで、いかがでしたでしょうか。
私は、この一連の話を知ってからは、今回のエンブレムが最高に思えて仕方ないです。
今では色々な意味で、実に日本らしいと思っています。
こんな数理的なデザインが、他の案に埋もれなくて本当に良かったです。
学塾ヴィッセンブルク 朝倉智義
おまけ。
面白いので暇人はお試しあれ。
これでパズルを作った人もいるようです。