
あすなろ110 多面体
2020年2月11日投稿
2010.12号
このあすなろ通信では、これまで、かなり色々なジャンルの話を書いてきました。
しかし、それでもまだ、敢えて手を出していないネタはあります。
例えば機械工学とか。
いや、だって、燃焼室のS/V比とかアームの動く瞬間中心の話とかをしたって面白くないですよね。
ぼくは面白いのですが。
まあ、そんなわけで今回は、この紙上で初めて取り上げる分野の話をします。
それは、数学の話です。
……はい、そこ、露骨に嫌な顔をしない。
テーマは、多面体です。
多面体とは、平らな面だけでできている立体のことです。
その中で、すべて合同な正多角形で構成され、且つ全ての頂点が同じ形状になっているものを正多面体と呼びます。
要するに、同じ正三角形や同じ正方形だけでできた形などのことです。
正多面体は、全部で5種類あることが知られています。
というより、5種類しか存在しません。
では何故、5種類しか無いのか。
それを説明してみましょう。
簡単ですよ。
立体の頂点は、正多角形である面の、頂点が集まってできています。
例えば、正四面体の全ての頂点は、それぞれ正三角形の角が3つ集まってできています。
正三角形の角を4つずつ集めて作ると、正八面体ができます。
5つずつなら、正二十面体になります。
6つ集めると、……立体はできません。
正三角形の角は60度ですので、それを6つ集めると360度、つまり平面になって、立体の頂点じゃなくなってしまうからです。
もちろん、2つでも無理です。
ですから、正三角形で作られる正多面体は、以上の3種類しかない、とわかるのです。
面が正四角形=正方形の場合は、角3つなら大丈夫なのですが、4つ集めたところで360度になってしまうので、1種類しかありません。
正五角形を使っても1種類です。
正六角形は、1つの角が120度ありますので、3つ集めただけで平面になります。
ですから、正多面体は作れません。
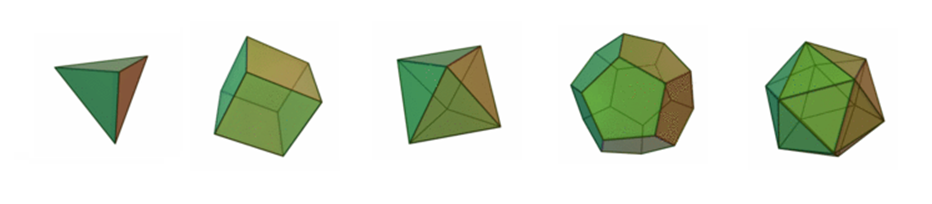
5種類の正多面体
左から順に、正四面体、正六面体、正八面体、正十二面体、正二十面体
こういうものって、文字で書くと伝わりにくいので、数字のお話はそのくらいにしましょう。
それよりも、その仲間達の話をします。
半正多面体というものがあります。
これは、定義が正多面体に近いのですが、面の形は正多角形であるならば、2種類以上が入っていてもいい、というものです。
これには一定の作り方があって、1つは、正多面体の角を、新しく正多角形ができるように切り落とす、という方法です。
もとからあった面の角を、辺の数が倍になるよう切ります。
すると、こんなものができます。
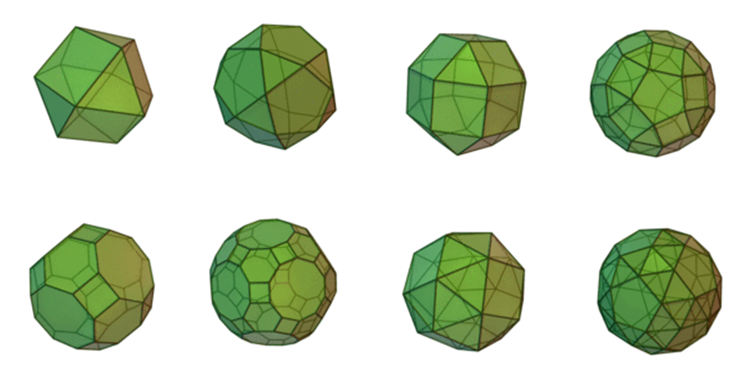
切頂シリーズ(「切隅」とも)
順に、切頂四面体、切頂六面体、切頂八面体、切頂十二面体、切頂二十面体

切り落とされた結果、正三角形、正四角形などの面は、正六角形、正八角形などへと変わっています。
また、切頂二十面体は、いわゆるサッカーボールの形ですよね。
つまりサッカーボール形は、正二十面体の頂点の数だけ正五角形ができている、ということです。
算数が好きな方は、辺と頂点の数を計算してみてください。
多分、小学三年生レベルの計算で、求められると思います。
次に挙げるのは、さらにこの切り落としを進めていった結果できた、半正多面体です。
そろそろややこしいので、解説は省きます。
切り落としの進め方
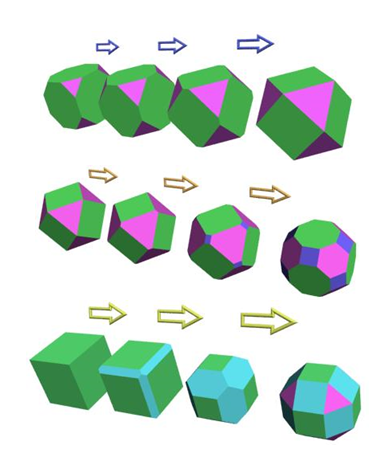
切る量をさらに進めていくと、切り落とした面同士が接するようになる。
場合によっては、さらに新たな頂点を切り落とす
その結果できた立体
そして、星形正多面体という恐ろしい立体もあります。
これは、正多角形の面を交差させながら組み合わせて作った形で、これまでに4種類だけが見つかっています。
4種類の星形正多面体
順に、大十二面体、大二十面体、小星形十二面体、大星形十二面体

このうち、大十二面体
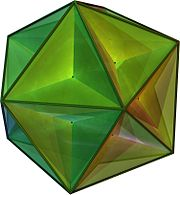
は、12枚の正五角形を、交差させながら組み合わせたものです。
1つの頂点には、正五角形の角が5つ、星形五角形(正5/2角形・五芒星)のように交差しながら集まっています。
上:星形五角形
下:晴明桔梗(家紋)

大二十面体

も同様に、正三角形を20枚、交差させながら組み合わせたものです。
その頂点は、これも同様に正三角形の角を星形五角形のように組み合わせています。
小星形十二面体

と、大星形十二面体

は、星形五角形を交差させながら組み合わせたものです。
頂点は、星形正五角形の角を3つまたは5つ集めたものです。
このくらいの立体になってくると、それなりの空間認識力が無いと、想像するのがそろそろきつくなってきます。
これの立体模型を作るのは困難でしょうが、針金を使って枠(辺)だけを作るのならできそうですね。
大人になって数学というと、苦手なイメージを持つ人が多いのですが、数学は学校で習う以外には、自ら学ぶ機会が殆ど無いからなのでしょうね。
学生の頃歴史が苦手だった人でも、その後本や会話で触れるうちに興味を持って、自分から調べて楽しくなることなんてあります。
しかし数学は、小説を読んでいたら新しい公式に興味が湧いてきた、なんてことは、普通はありませんからね。
でも、趣味で始めると、数学も案外面白いものですよ。
学問とは、そういうものです。
学塾ヴィッセンブルク 朝倉智義