2021年12月
2021.11 小5向け茨城県立中学校・中等教育学校(中高一貫校)適性検査合格推定偏差値
(2021.12.13のブログとほぼ同じです)
11月に行われた公中検オープン模試で、
5年生の書いた志望校とその結果から、
近隣の、県立中学推定偏差値を出してみました。
あくまで、推定の偏差値ですが、
ちょうど来年度受験の倍率が出ましたので、
それをフィードバックさせてみました。
ただし、模試屋さんの出す偏差値のような、
追跡調査のデータから出したものではありませんので、
まあ、その程度のものだと思ってくだされば。
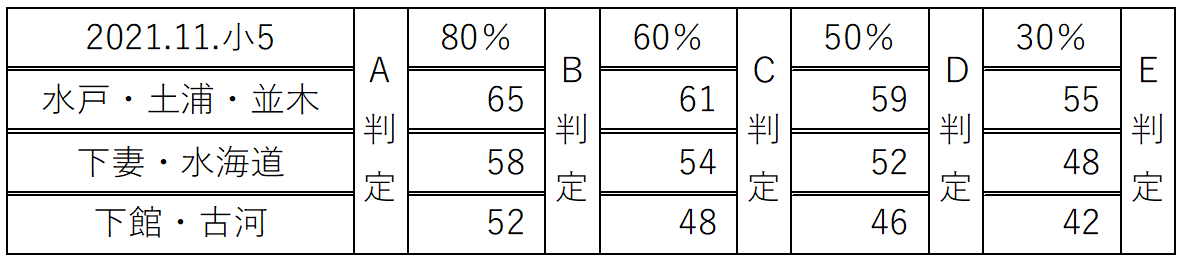
2021.11.公中検模試:小5
水戸一・土浦一・並木
80%偏差値:65
60%偏差値:61
50%偏差値:59
30%偏差値:55
下妻一・水海道一
80%偏差値:58
60%偏差値:54
50%偏差値:52
30%偏差値:48
下館一・古河
80%偏差値:52
60%偏差値:48
50%偏差値:46
30%偏差値:42
80%~ :A判定
60~79%:B判定
50~59%:C判定
30~49%:D判定
~29% :E判定
上にあるとおり、このデータは
公中検模試2021年11月の、小5限定です。
大抵の模試は、このような結果は、模試屋さんが追跡調査の結果から算出するものなのですが、
公中検模試では、こういう数値を発表しておりません。
(イバシンのそっくり模試も同じです)
そこで、当塾では自分で出しております。
当塾がやっている「公中検オープン」は、
毎回、送られてきた成績表と一緒に、こういうデータをつけてお渡ししています。
普段は、受験者だけに配布して終わりなのですが、
ブログで書いたところ好評でしたので、ちょっと出してみました。
(今後は出さないかもしれません)
信用度……を突かれると、ちょっと自信はないのですが、
下館一高附属の倍率については、
前年2.45から1.8に下がるだろうと6年生のデータから算出したところ、
実際に1.88と、ほぼ的中でした。
ですから上の偏差値も案外、いいところかもしれません。
ただし、今回の倍率を見て、今後どう動くかはわかりません。
ですからあくまでも、2021年11月時点での、小5限定とします。
2021年度 入試結果

----------2021年度入試結果----------
◆◆◆ 小学生:中学受験/受検 ◆◆◆
(合格数 / 受験数)
・土浦第一高等学校附属中学校
→ 1/1(100%)
・下館第一高等学校附属中学校
→ 1/1(100%)
・並木中等教育学校
→ 1/3(33%)
・古河中等教育学校
→ 3/4(75%)
・茗溪学園中学校
→ 1/2(50%)
・常総学院中学校
→ 1/1(100%)
中学受験合計
→ 8/12(67%)
他塾の合格率と比較できるように、全人数を書き出しています。
◆◆◆ 中学生:高校受験 ◆◆◆
(進学先のみ)
・土浦第一高等学校
→ 1/1
・下妻第一高等学校
→ 1/1
・水海道第一高等学校
→ 1/1
・境高等学校
→ 1/1
・常総学院高等学校
→ 1/1
・國學院大學栃木高等学校
→ 1/1
・その他、滑り止め
以上、全て第一志望に合格。
滑り止めも含め、合格率100%です。
最近3年間の累計では、
県立受験者26人中、17人(65.4%)が
下妻一高に進学しました。
また、下妻一高と同等以上の高校
(下館一・下妻一・水海道一・土浦一・竹園・小山高専)へは、
全受験生の84.6%が進学をしています。
◆◆◆ 高校生:大学受験 ◆◆◆
(判明分)
・名古屋大学
・東京農業大学
・専修大学
・東洋大学
・帝京大学
・千葉工業大学
・その他
ありがとうございました。
2020年度 入試結果

-----2020年度入試結果-----
◆◆◆小学生:中学受験/受検(全3人)◆◆◆
・東京大学教育学部附属中等教育学校 ×1
・古河中等教育学校 ×2
「古河中等合格100%」を
うたっている塾があるようですね。
当塾も、そう書いたことがあります。
※ ちなみに、1人受けて1人合格でも100%です。
◆◆◆中学生:高校受験(全11人)◆◆◆
・小山工業高等専門学校 ×1
・下妻第一高等学校 ×8
・下館第一高等学校 ×2
……その他、本命以外の私立高
おかげさまで高校受験は、最近3年間を累計しますと
26人中19人(73%)が下妻一高に進学しました。
(下館一・土浦一・小山高専も合わせると92%です)
また2019年度は、受験生(8人)の100%が下妻一高へ進学しています。
◆◆◆高校生:大学受験(全9人)◆◆◆
・千葉大学 ×1
・琉球大学 ×1
・前橋工科大学 ×1
・明治大学 ×1
・東京理科大学 ×1
・順天堂大学 ×1
・東洋大学 ×2
・武蔵野美術大学 ×1
・多摩美術大学 ×1
・明星大学 ×1
……他、滑り止めなど
ありがとうございました。
2020県立中適性検査I-1(1)の解説
2020年度茨城県立中等教育学校適性検査の、大問1(1)の解説記事です。

(生徒の使った問題用紙をそのままコピーしています)
私が思いついた解法は3つです。
1.立体の面の構成を読み取って計算する
(多分これが正攻法)
図を見ると、正六角形を構成する辺は、3本が隣の六角形と接して、残り3本が正五角形と接しています。
つまり、正五角形の辺3本につき、正六角形が1枚できる、と考えることができます。
正五角形は12枚ですので、その辺の総数は、
12×5=60
この60本の辺で、3本につき1枚の六角形が作られるので、
60÷3=20
よって20枚。
2.多面体についての知識から解く
(数学マニアな小学生なら知っているかもしれない)
サッカーボールの形は、切頂正二十面体と呼ばれていまして、正二十面体の頂点を切り落とした形です。
正二十面体の頂点は、正三角形5枚から構成されていますので、それを切ると正五角形の断面ができます。
切る深さを調整して、角を落とされた正三角形の各面が正六角形になるようにすれば、いわゆるサッカーボール型ができます。
問題文の通り、正五角形が12枚なのは、正二十面体の頂点が12個だからです。
そして正六角形の面は、もとは正二十面体の面なのですから、そのまま20枚となります。
3.絵を見て数える
今回の問題にある、手に持ったサッカーボールのイラスト(図1)は、手で隠れている部分を推測すれば、白い面が10枚あると数えられます。
反対側からも同じものが見えるとすれば、
10×2=20
以上。
※
ズルかと思われるでしょうが、問題文をよく読むと、今回の問題は「数を書きなさい」であって、考え方の説明は不要だということがわかります。
つまり、答えの数値さえ出ればそれでいいのです。
何が何でも答えを出す、という気概があるなら、私はこういう解法も否定しません。
おそらく、図1だけではすぐに数えられてしまうので、それを惑わせるために図2が追加されたのでしょう。
よくできた問題だと思います。
さて、そんな話を古河中等の生徒としていたら、もう一つ解法があると言われました。
4.オイラーの多面体定理を使う
(多分小学生は知らないかと……)
この定理を使うためには辺の数と頂点の数が必要なのですが、図を見れば辺の数も確かに計算できそうです。
が、ちょっと飛び道具過ぎるので詳細は略します。
以上。
いかがでしょうか。
※参考までに、当塾生の反応
(全員に聞いたわけではありません)
・土浦一高3年は、2.の解法で解きました。
・竹園高3年は、1.の解法で解きました。
・古河中等4年(高1)は、2.で解いてから上記の通り4.を提案しました。
・普通の中学の中3は、解けませんでした。
・古河中等2年(中2)は、解けませんでした。
まあ、解けなくても大丈夫ですので。
7の倍数判別法
倍数判別法というものがあります。
2の倍数:下一桁が偶数
5の倍数:下一桁が0か5
くらいはすぐにわかると思いますが、
それ以外でも、
4の倍数:下二桁が4の倍数
8の倍数:下三桁が8の倍数
3の倍数:各位の数字の和が3の倍数
9の倍数:各位の数字の和が9の倍数
6の倍数:3の倍数で偶数
あたりは、中学受験用のテキストには載っています。
問題は、7の倍数です。
インターネット上には、これの見つけ方があるらしいのですが、聞く話によると、どうも計算が大変らしいです。
で、1ヶ月ほど前、茗溪の宿題をヒントに考えてみました。
そうしたら、かけ算九九と大きい数の引き算さえできれば算出できる方法を見つけましたので、ここに上げておきます。
ご自由にお使いください。
学塾ヴィッセンブルク 朝倉智義
